The Elo Rating System in the MLB • Linell Bonnette

Have you ever wondered how to predict the outcome of a baseball game? You’ve almost definitely seen the “Matchup Predictor” on ESPN, or similar features on other sports sites. The percentages shown aren’t random guesses nor are they based on anything more magical than math.

What is the Elo Rating System?

Wikipedia says:

The Elo rating system is a method for calculating the relative skill levels of players in zero-sum games such as chess or esports. It is named after its creator Arpad Elo, a Hungarian-American physics professor.

The difference in the ratings between two players serves as a predictor of the outcome of a match. Two players with equal ratings who play against each other are expected to score an equal number of wins. A player whose rating is 100 points greater than their opponent’s is expected to score 64%; if the difference is 200 points, then the expected score for the stronger player is 76%.

After every game, the winning player takes points from the losing one. The difference between the ratings of the winner and loser determines the total number of points gained or lost after a game. If the higher-rated player wins, then only a few rating points will be taken from the lower-rated player. However, if the lower-rated player scores an upset win, many rating points will be transferred. The lower-rated player will also gain a few points from the higher rated player in the event of a draw. This means that this rating system is self-correcting.

Elo ratings are comparative only, and are valid only within the rating pool in which they were calculated, rather than being an absolute measure of a player’s strength.

Let’s Do It

Amy Langville’s book, Who’s #1? The Science of Rating and Ranking is a great resource for understanding the Elo rating system. I’m going to largely assume that, if you’re using this post to create your own ratings, you’ve either already read the book or are mathy enough to follow along.

What Data Do We Need?

The Elo rating system doesn’t require a bunch of fancy data — just the teams and the outcomes of the games that they’ve played. I’ve created a little SQLite database with game outcomes that you can download here, but using your own data should be straightforward.

The Math

The ratings system is based on the idea that the difference in ratings between two teams is a good predictor of a contest’s outcome. The formula for the expected score for team A is:

E_A = \frac{1}{1 + 10^{(\frac{R_B - R_A}{400})}}

where

R_A

is the rating of team A and

R_B

is the rating of team B.

This formula is a way to estimate how likely one team, A, is to win against another team, B, based only on their current ratings.

Whenever the teams plays a new contest, we update their ratings to reflect the outcome. The new rating for team A is:

R_{new} = R_{old} + K \times (S - E)

where

K is a constant that you can set to whatever you want, and it’s used to determine how much the rating should change based on the outcome of the game. This is one of the more tweakable parts of the rating system, and people have many opinions on how to it’s best set.
S is the actual result of the game, which is 1 for a win, 0.5 for a tie, and 0 for a loss.
E is the expected result of the game, which is calculated using the formula above.

Everyone starts with the same rating, often 1500. This value is arbitrary, and you can set it to whatever you want. In that same vein, the value of 400 in the denominator of the expected score formula is arbitrary¹. The value of 400 was chosen by Arpad Elo himself to help keep the ratings compatible with the prior chess rating system, designed by Kenneth Harkness.

The Code

The code isn’t very complicated, but it is a bit long. I’ve created a gist that you can view here, where there’s a basic EloRatingSystem Python class that is used for calculating ratings based off of the historical data from above.

How Well Does it Work?

I played around with the data and code above and created the chart below, showing the accuracy of the system on this dataset over time.

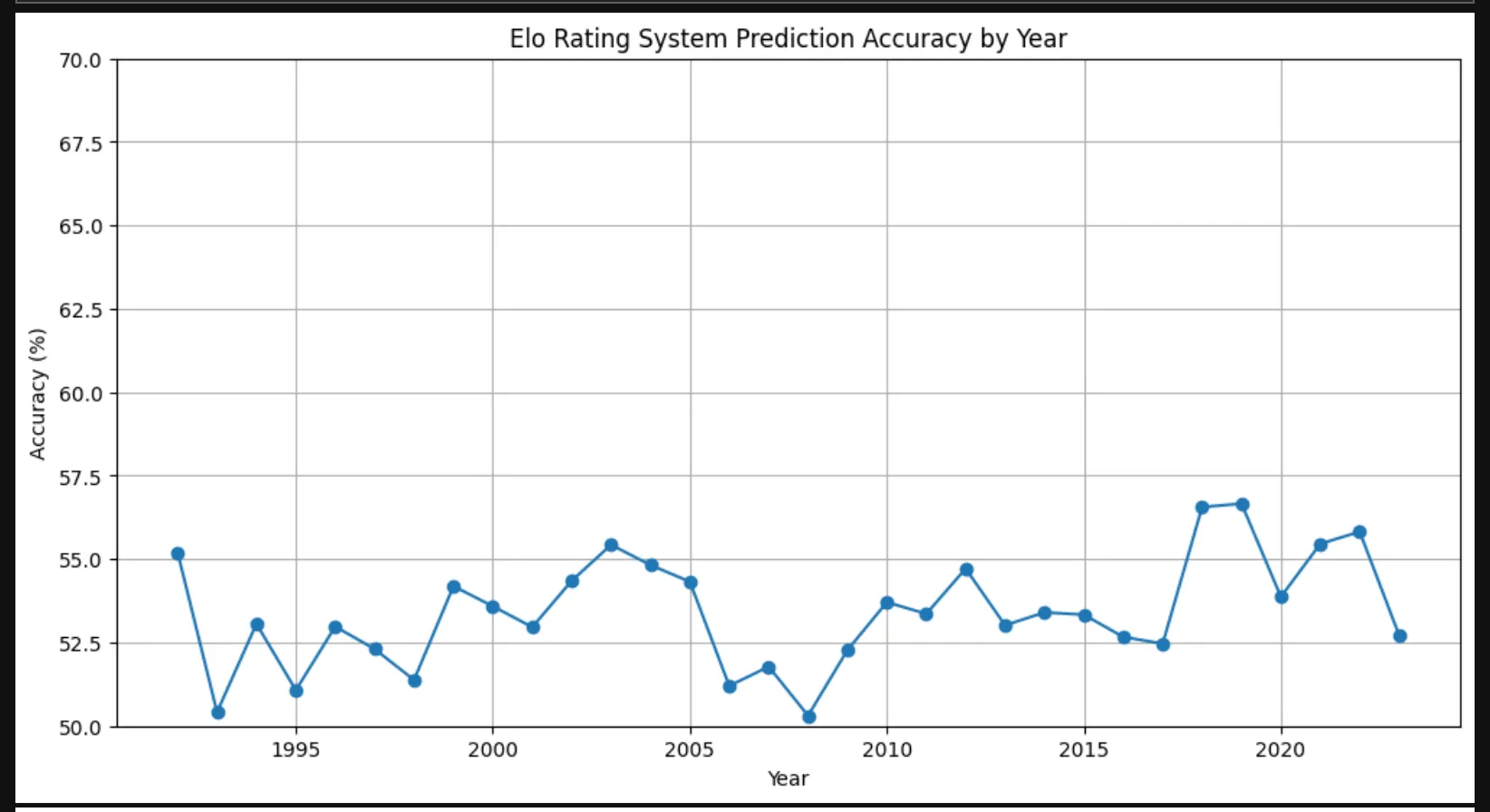
Anecdotally, I’ve seen the system do a respectable job of predicting contest outcomes. It’s far from perfect, but it’s a fun and relatively simple way to get started with ratings and predictions.

Footnotes

“Where do the default values in the Elo ratings formulas come from?” on StackExchange ↩